Continuity
In mathematics, continuity refers to the smoothness or uninterrupted nature of a function. A function is said to be continuous if it can be drawn without lifting the pen from the paper. This means that there are no breaks, jumps, or holes in the graph of the function.
Key Concepts:
- Continuity of a Function: A function f(x) is continuous at a specific point c if the following conditions are met:
- f(c) is defined (i.e., the function exists at c)
- The limit of f(x) as x approaches c exists
- The limit of f(x) as x approaches c is equal to f(c)
- Types of Discontinuities: There are several types of discontinuities, including:
- Removable Discontinuity
- Jump Discontinuity
- Infinite Discontinuity
- Continuity on an Interval: A function is said to be continuous on a closed interval [a, b] if it is continuous at every point in the interval and at the endpoints a and b.
Study Guide:
Here are some key points to remember when studying continuity:
- Understand the concept of continuity and what it means for a function to be continuous at a point.
- Learn how to identify different types of discontinuities and understand their graphical representations.
- Practice determining the continuity of a function on a given interval by checking the conditions for continuity at each point in the interval.
- Work on problems involving limits to strengthen your understanding of continuity and its relationship to the behavior of functions.
- Use graphing tools to visualize the continuity of functions and identify points of discontinuity.
Remember to practice solving problems related to continuity to reinforce your understanding of the concept.
.◂Science Worksheets and Study Guides Second Grade. Comparing matter
Study Guide Comparing matter
Comparing matter  Activity Lesson
Activity Lesson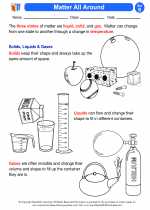 Matter All Around
Matter All Around  Worksheet/Answer key
Worksheet/Answer key Comparing matter
Comparing matter  Worksheet/Answer key
Worksheet/Answer key Comparing matter
Comparing matter  Worksheet/Answer key
Worksheet/Answer key Comparing matter
Comparing matter  Vocabulary/Answer key
Vocabulary/Answer key Comparing matter
Comparing matter 

 Activity Lesson
Activity Lesson
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key

The resources above cover the following skills:
PHYSICAL SCIENCE (NGSS)
Matter and its Interactions
Students who demonstrate understanding can:
Construct an argument with evidence that some changes caused by heating or cooling can be reversed and some cannot.