Continuity in Mathematics
Continuity is a fundamental concept in mathematics, particularly in the field of calculus. It refers to the smooth and unbroken nature of a function or a curve. When a function is continuous, it means that there are no sudden jumps, breaks, or holes in its graph.
Defining Continuity
A function f(x) is continuous at a point c if the following three conditions are met:
- f(c) is defined (i.e., the function is defined at the point c).
- The limit of f(x) as x approaches c exists.
- The limit of f(x) as x approaches c is equal to f(c) (i.e., the function value at c).
Types of Discontinuities
While continuity implies a smooth and unbroken graph, there are certain types of discontinuities that can occur in functions:
- Removable Discontinuity: This occurs when there is a hole in the graph of the function at a certain point, but the function can be made continuous by defining its value at that point.
- Jump Discontinuity: In this case, the function "jumps" from one value to another at a specific point, creating a visible gap in the graph.
- Infinite Discontinuity: When the function approaches positive or negative infinity at a certain point, it results in an infinite discontinuity.
- Essential Discontinuity: This type of discontinuity is more complex and typically involves oscillations or irregular behavior near a specific point.
Continuity Study Guide
When studying continuity in mathematics, it's important to focus on the following key concepts:
- Understanding the definition of continuity and being able to identify whether a function is continuous at a given point.
- Recognizing the different types of discontinuities and understanding how they manifest in the graph of a function.
- Practicing the application of continuity in solving problems related to limits, derivatives, and integrals in calculus.
- Exploring real-world examples where continuity is relevant, such as in the analysis of physical phenomena or engineering designs.
By mastering the concept of continuity, you'll develop a strong foundation for more advanced topics in calculus and mathematical analysis.
.◂Science Worksheets and Study Guides Sixth Grade. Magnetism
Study Guide Magnetism
Magnetism  Activity Lesson
Activity Lesson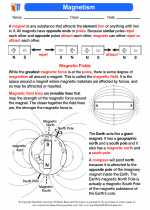 Magnetism
Magnetism  Worksheet/Answer key
Worksheet/Answer key Magnetism
Magnetism  Worksheet/Answer key
Worksheet/Answer key Magnetism
Magnetism  Worksheet/Answer key
Worksheet/Answer key Magnetism
Magnetism  Worksheet/Answer key
Worksheet/Answer key Magnetism
Magnetism  Vocabulary/Answer key
Vocabulary/Answer key Magnetism
Magnetism 

 Activity Lesson
Activity Lesson
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key

The resources above cover the following skills:
EARTH AND SPACE SCIENCE
Earth’s Systems
Develop and use models of Earth’s interior composition to illustrate the resulting magnetic field (e.g., magnetic poles) and to explain its measureable effects (e.g., protection from cosmic radiation).