Domain in Mathematics
In mathematics, the term "domain" refers to the set of all possible input values (x-values) for which a function is defined. It is the set of all real numbers for which the function is defined and can produce a valid output. The domain is a fundamental concept in understanding functions and their behavior.
Understanding Domain
When working with functions, it is important to understand the domain to ensure that the function is valid for all possible input values. The domain of a function can be restricted by certain mathematical operations or restrictions within the function itself.
For example, consider the function f(x) = √(x). In this case, the domain of the function is all real numbers greater than or equal to zero, since the square root of a negative number is not a real number. Therefore, the domain of this function is [0, ∞).
How to Determine the Domain
To determine the domain of a function, you need to consider any restrictions on the input values that would make the function undefined. Common restrictions include:
- Radical expressions: For functions involving square roots or other even roots, the radicand (the expression inside the radical) must be greater than or equal to zero to ensure a real number output.
- Fractional expressions: For functions involving fractions, the denominator must not be equal to zero, as division by zero is undefined.
- Logarithmic expressions: For functions involving logarithms, the argument of the logarithm must be greater than zero to ensure a real number output.
- Trigonometric expressions: For trigonometric functions, certain input values may result in undefined outputs due to singularities or asymptotes.
Study Guide
Here are some key points to remember when studying the domain of a function:
- Understand the basic concepts of functions and their definitions.
- Identify the type of function you are dealing with (e.g., polynomial, rational, exponential, logarithmic, trigonometric).
- Be aware of common restrictions for each type of function that affect the domain.
- Practice determining the domain of various functions by identifying restrictions and considering the set of all valid input values.
- Use graphing tools or software to visualize the domain of functions and understand how different input values affect the output.
By mastering the concept of domain, you will gain a deeper understanding of how functions behave and the limitations of their input values.
.◂Science Worksheets and Study Guides Seventh Grade. Cell Processes

 Activity Lesson
Activity Lesson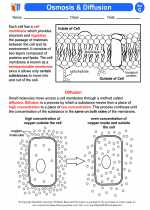
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
