Calculus
Calculus is a branch of mathematics that deals with the study of rates of change and accumulation. It has two major branches: differential calculus, which involves the study of the rates at which quantities change; and integral calculus, which involves the study of the accumulation of quantities.
Differential Calculus
Differential calculus is concerned with the study of how a function changes as its input changes. The key concept in differential calculus is the derivative, which measures the rate of change of a function at a particular point. The derivative of a function f(x) is denoted as f'(x) or dy/dx, and it represents the slope of the tangent line to the graph of the function at a given point.
Integral Calculus
Integral calculus focuses on the accumulation of quantities and the computation of areas and volumes. The central concept in integral calculus is the integral, which represents the accumulation of a quantity over a range. The definite integral of a function f(x) over the interval [a, b] is denoted as ∫[a, b] f(x) dx, and it represents the signed area between the x-axis and the curve of the function between the limits a and b.
Study Guide for Calculus
- Understand the concept of limits and continuity in functions.
- Learn how to find derivatives using the power rule, product rule, quotient rule, and chain rule.
- Practice finding the second derivative and understanding its significance in analyzing the concavity of a function.
- Explore applications of derivatives, such as optimization problems and related rates problems.
- Study techniques for finding antiderivatives and definite integrals, including the fundamental theorem of calculus.
- Practice solving problems involving areas between curves, volumes of solids of revolution, and work problems using integrals.
Calculus is a fundamental tool in various fields such as physics, engineering, economics, and computer science. Mastering the concepts and techniques of calculus can provide a strong foundation for further studies in these areas.
.◂Science Worksheets and Study Guides Seventh Grade. Ecosystems, food chains and food webs

 Activity Lesson
Activity Lesson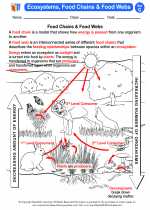
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
