Angular Velocity
Angular velocity is a measure of how quickly an object is rotating around a particular point or axis. It is a vector quantity, meaning it has both magnitude and direction.
The formula for angular velocity (ω) is given by:
ω = Δθ / Δt
To calculate the average angular velocity, use the formula:
ω(avg) = (θf - θi) / (tf - ti)
Angular velocity is an important concept in physics and engineering, as it is used to describe the rotational motion of objects such as wheels, propellers, and gears. It is also a key parameter in understanding the motion of celestial bodies, such as planets and stars.
Study Guide
- Definition: Understand the definition of angular velocity as the rate of change of angular displacement with respect to time.
- Units: Learn the units of angular velocity, which are radians per second (rad/s).
- Calculation: Practice using the formula for angular velocity to solve problems involving rotational motion.
- Relationship to linear velocity: Understand the relationship between linear velocity (v) and angular velocity (ω), given by the formula v = rω, where r is the radius of the circular path.
- Applications: Explore real-world applications of angular velocity, such as in machinery, vehicle dynamics, and astronomy.
- Direction: Remember that angular velocity is a vector quantity and has both magnitude and direction. It follows the right-hand rule, where the direction of the angular velocity vector is perpendicular to the plane of rotation, pointing in the direction of the axis of rotation.
◂Biology Worksheets and Study Guides High School. Human biology I
Worksheet/Answer key Human biology I
Human biology I  Worksheet/Answer key
Worksheet/Answer key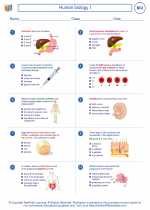 Human biology I
Human biology I  Worksheet/Answer key
Worksheet/Answer key Human biology I
Human biology I  Worksheet/Answer key
Worksheet/Answer key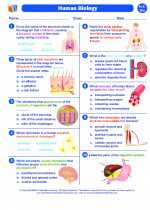 Human biology I
Human biology I  Vocabulary/Answer key
Vocabulary/Answer key Human biology I
Human biology I  Vocabulary/Answer key
Vocabulary/Answer key Human biology I
Human biology I  Vocabulary/Answer key
Vocabulary/Answer key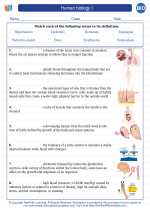 Human biology I
Human biology I  Vocabulary/Answer key
Vocabulary/Answer key Human biology I
Human biology I  Vocabulary/Answer key
Vocabulary/Answer key Human biology I
Human biology I  Vocabulary/Answer key
Vocabulary/Answer key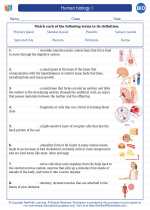 Human biology I
Human biology I  Vocabulary/Answer key
Vocabulary/Answer key Human biology I
Human biology I 

 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key

The resources above cover the following skills:
LIFE SCIENCE (NGSS)
From Molecules to Organisms: Structures and Processes
Students who demonstrate understanding can:
Develop and use a model to illustrate the hierarchical organization of interacting systems that provide specific functions within multicellular organisms.
Plan and conduct an investigation to provide evidence that feedback mechanisms maintain homeostasis.