Key Concepts in Geometric Optics
Light Reflection
Light reflection occurs when light bounces off a surface. The angle of incidence is equal to the angle of reflection, and this principle forms the basis of understanding how mirrors create images.
Mirror Equation
The mirror equation, 1/f = 1/do + 1/di, relates the focal length (f), object distance (do), and image distance (di) for concave and convex mirrors. Understanding this equation helps in predicting the characteristics of images formed by mirrors.
Lens Equation
The lens equation, 1/f = 1/do + 1/di, is used to relate the focal length (f), object distance (do), and image distance (di) for convex and concave lenses. It allows for the prediction of image formation by lenses.
Image Formation
Understanding how images are formed by mirrors and lenses, including the concepts of real and virtual images, magnification, and the nature of the images formed, is crucial in geometric optics.
Ray Diagrams
Creating and interpreting ray diagrams for mirrors and lenses is a fundamental skill. Ray diagrams help visualize how light behaves as it interacts with optical systems, leading to the formation of images.
Optical Systems
Understanding how multiple mirrors and lenses can be combined to form complex optical systems is essential. This includes understanding the principles of telescopes, microscopes, and other optical instruments.
Study Tips
- Practice drawing ray diagrams for different types of mirrors and lenses.
- Understand the sign conventions for the various parameters in mirror and lens equations.
- Work through example problems to solidify your understanding of image formation by mirrors and lenses.
- Explore real-world applications of geometric optics, such as in the design of eyeglasses, cameras, and telescopes.
- Review the differences between concave and convex mirrors, as well as between concave and convex lenses, in terms of their image-forming characteristics.
◂Science Worksheets and Study Guides Sixth Grade. Introduction to earth science

 Activity Lesson
Activity Lesson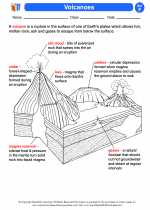
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
