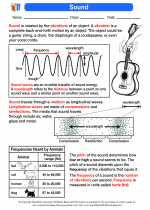
Sound -> continuity
Continuity in Mathematics
Continuity is a fundamental concept in mathematics, especially in the study of functions and calculus. A function is said to be continuous at a point if it is defined at that point and if the limit of the function as it approaches that point exists and is equal to the value of the function at that point.
Definition of Continuity
A function f(x) is continuous at a point c if the following three conditions are met:
- f(c) is defined (i.e., the function is defined at c).
- The limit of f(x) as x approaches c exists.
- The limit of f(x) as x approaches c is equal to f(c).
Types of Discontinuities
There are several types of discontinuities that a function can exhibit:
- Removable Discontinuity: This occurs when a function has a hole or gap at a certain point, but it can be filled in to make the function continuous at that point.
- Jump Discontinuity: This occurs when the left-hand and right-hand limits at a certain point exist, but they are not equal.
- Infinite Discontinuity: This occurs when the limit of the function at a certain point approaches positive or negative infinity.
- Essential Discontinuity: This occurs when a function has a non-removable discontinuity at a certain point.
Continuity Study Guide
To study continuity, it is important to understand the following key concepts:
- Limits: Understand the concept of limits and how they relate to the continuity of a function.
- Definition of Continuity: Memorize the conditions for a function to be continuous at a point.
- Types of Discontinuities: Be able to identify and differentiate between the various types of discontinuities.
- Graphical Analysis: Practice analyzing the graphs of functions to determine their continuity and identify any discontinuities.
Continuity is a crucial concept in calculus and is essential for understanding the behavior of functions. Mastery of this topic will lay a strong foundation for further studies in mathematics.