Factoring
Factoring is the process of finding the numbers or algebraic expressions that multiply together to give a particular number or expression. It is an important concept in mathematics and is used in various areas such as algebra, number theory, and calculus.
Types of Factoring
There are several types of factoring, including:
- Factorization of Integers: Finding the prime factors of a given integer. For example, the prime factorization of 12 is 2 * 2 * 3.
- Factoring Algebraic Expressions: Breaking down algebraic expressions into simpler factors. For example, factoring the expression x^2 - 4 results in (x - 2)(x + 2).
- Factoring Quadratic Expressions: Finding the factors of quadratic expressions of the form ax^2 + bx + c. For example, factoring the expression x^2 + 5x + 6 results in (x + 2)(x + 3).
Methods of Factoring
There are various methods for factoring algebraic expressions, including:
- Common Factor: Factoring out the greatest common factor from an expression.
- Factoring by Grouping: Grouping terms in an expression and factoring common factors from each group.
- Factoring Quadratic Expressions: Using methods such as the difference of squares, perfect square trinomials, and the quadratic formula to factor quadratic expressions.
Study Guide
To master the concept of factoring, it is important to:
- Understand the basic principles of multiplication and division.
- Be familiar with prime numbers and prime factorization.
- Practice factoring integers and algebraic expressions using various methods.
- Learn and apply the techniques for factoring quadratic expressions.
- Solve plenty of practice problems to reinforce the understanding of factoring.
Understanding factoring is crucial for solving equations, simplifying expressions, and working with polynomial functions. It is a fundamental skill that is used extensively in higher-level math courses.
By mastering the concept of factoring, you will be better equipped to tackle more complex mathematical problems and build a strong foundation for future math studies.
.◂Math Worksheets and Study Guides Fourth Grade. Lines and Angles

 Study Guide
Study Guide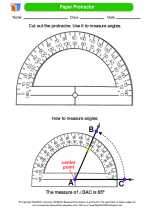
 Activity Lesson
Activity Lesson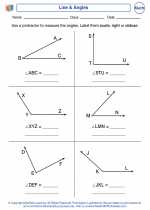
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
