Hexagonal Tessellation
A hexagonal tessellation is a pattern of regular hexagons that fit together without any gaps or overlaps to cover a plane. This type of tessellation is created by repeating a single hexagon shape over and over again, filling the entire plane without leaving any spaces.
Characteristics of Hexagonal Tessellation
- Regular Hexagons: The tessellation is made up of regular hexagons, meaning all the sides and angles of the hexagons are equal.
- No Gaps or Overlaps: The hexagons fit together perfectly without leaving any gaps or overlapping each other.
- Rotational Symmetry: The tessellation exhibits rotational symmetry, as the pattern can be rotated and still look the same.
How to Create a Hexagonal Tessellation
To create a hexagonal tessellation, you can start with a single regular hexagon and then repeat it in a specific pattern to fill the plane. One way to do this is by using a "three around one" pattern, where each hexagon is surrounded by three other hexagons. This creates a repeating pattern that covers the entire plane without any gaps or overlaps.
Applications of Hexagonal Tessellation
Hexagonal tessellations can be found in various real-world applications, including:
- Tile Patterns: Many floor and wall tile designs use hexagonal tessellations to create visually appealing patterns.
- Honeycomb Structures: The natural structure of honeycombs is a hexagonal tessellation, providing strength and efficiency in storing honey.
- Geometric Art: Artists and designers often use hexagonal tessellations as a basis for creating intricate geometric patterns and artwork.
Study Guide
To understand hexagonal tessellation, it's important to focus on the following key points:
- Understanding the properties of regular hexagons, including their angles and side lengths.
- Exploring the concept of tessellation and how shapes can be repeated to cover a plane without any gaps or overlaps.
- Identifying and creating patterns of hexagonal tessellations using a "three around one" approach.
- Recognizing real-world examples of hexagonal tessellations and their applications in various fields.
By mastering these concepts, you will develop a solid understanding of hexagonal tessellation and its significance in mathematics and the real world.
.◂Math Worksheets and Study Guides Fourth Grade. Lines and Angles

 Study Guide
Study Guide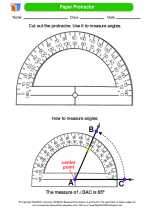
 Activity Lesson
Activity Lesson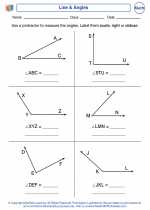
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
