Right Triangle Study Guide
A right triangle is a type of triangle that has one angle measuring 90 degrees. This angle is called the right angle.
Properties of a Right Triangle:
- A right triangle has three sides: the hypotenuse, the opposite side, and the adjacent side.
- The side opposite to the right angle is called the hypotenuse.
- The side next to the right angle is called the adjacent side.
- The side opposite to the angle other than the right angle is called the opposite side.
Pythagorean Theorem:
The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
Mathematically, this can be represented as: a2 + b2 = c2, where c is the length of the hypotenuse, and a and b are the lengths of the other two sides.
Special Right Triangles:
There are two special types of right triangles: 45-45-90 triangle and 30-60-90 triangle. In a 45-45-90 triangle, the two legs are congruent, and in a 30-60-90 triangle, the sides are in a ratio of 1:2:√3.
Practice Problems:
1. In a right triangle, if the lengths of the two legs are 3 and 4, what is the length of the hypotenuse?
2. In a 45-45-90 triangle, if one leg has a length of 5, what are the lengths of the other leg and the hypotenuse?
Answers:
1. Using the Pythagorean theorem, the length of the hypotenuse can be calculated as: √(32 + 42 2. In a 45-45-90 triangle, the lengths of the legs and the hypotenuse are equal, so the other leg and the hypotenuse both have a length of 5√2
◂Math Worksheets and Study Guides Fifth Grade. Percents

 Activity Lesson
Activity Lesson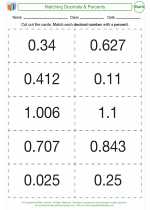
 Activity Lesson
Activity Lesson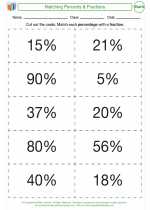
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
