Tangent
In mathematics, the tangent of an angle in a right-angled triangle is a ratio that relates the length of the side opposite the angle to the length of the side adjacent to the angle. The tangent function is denoted as tan.
Definition
The tangent of an angle θ is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle, in a right-angled triangle.
Mathematically, the tangent of an angle θ is given by:
tan(θ) = Opposite side / Adjacent side
Key Concepts
1. Right-Angled Triangle: The tangent function is applicable to right-angled triangles, where one of the angles is 90 degrees.
2. Opposite and Adjacent Sides: The sides of the triangle with respect to the angle are referred to as the opposite side and the adjacent side, based on the position of the angle.
3. Range of Values: The tangent function can take any real number as its input and gives a real number as its output.
Usage
The tangent function is widely used in trigonometry, physics, engineering, and various other fields to solve problems related to angles and distances. It helps in finding unknown sides or angles in a right-angled triangle and is a fundamental concept in the study of trigonometry.
Study Guide
When studying the tangent function, it's important to focus on the following key points:
- Understanding the definition of the tangent function and how it relates to right-angled triangles.
- Identifying the opposite and adjacent sides in a right-angled triangle with respect to a given angle.
- Practicing the use of the tangent function to solve for unknown sides or angles in a right-angled triangle.
- Exploring real-world applications and problem-solving scenarios where the tangent function is used.
By mastering these concepts, you'll build a strong foundation in trigonometry and be able to apply the tangent function to various mathematical and practical problems.
.◂Math Worksheets and Study Guides Fifth Grade. Percents

 Activity Lesson
Activity Lesson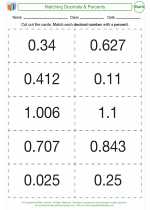
 Activity Lesson
Activity Lesson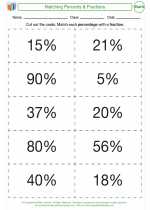
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key
