Quotient Rule
The quotient rule is a formula used to find the derivative of a function that is the quotient of two other functions.
Formula
The quotient rule is given by:
f'(x) = (g(x) * f'(x) - f(x) * g'(x)) / (g(x))^2
Where:
- f(x) is the numerator function
- g(x) is the denominator function
- f'(x) is the derivative of the numerator function
- g'(x) is the derivative of the denominator function
Example
Let's find the derivative of the function f(x) = (2x + 1) / (x^2 + 3x + 2).
Using the quotient rule, we have:
f'(x) = ((x^2 + 3x + 2)*(2) - (2x + 1)*(2x + 3)) / (x^2 + 3x + 2)^2
After simplifying, we get the derivative:
f'(x) = (2x^2 + 6x + 4 - 4x^2 - 6x - 2) / (x^2 + 3x + 2)^2
f'(x) = (-2x^2 - 2) / (x^2 + 3x + 2)^2
Study Guide
To use the quotient rule, follow these steps:
- Identify the numerator function f(x) and the denominator function g(x).
- Find the derivatives f'(x) and g'(x) of the numerator and denominator functions, respectively.
- Apply the quotient rule formula to find the derivative f'(x) of the original function.
Remember to always simplify your final answer if possible, and be careful with the signs when using the quotient rule.
.◂Math Worksheets and Study Guides Seventh Grade. Finding Volume
Study Guide Finding Volume
Finding Volume  Activity Lesson
Activity Lesson Volume Cubes
Volume Cubes  Activity Lesson
Activity Lesson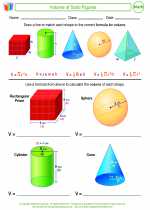 Volume of Solid Figures
Volume of Solid Figures  Activity Lesson
Activity Lesson Volume Problem
Volume Problem  Worksheet/Answer key
Worksheet/Answer key Finding Volume
Finding Volume  Worksheet/Answer key
Worksheet/Answer key Finding Volume
Finding Volume  Worksheet/Answer key
Worksheet/Answer key Finding Volume
Finding Volume  Worksheet/Answer key
Worksheet/Answer key Finding Volume
Finding Volume 

 Activity Lesson
Activity Lesson
 Activity Lesson
Activity Lesson
 Activity Lesson
Activity Lesson
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key

The resources above cover the following skills:
Geometry (NCTM)
Analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships.
Precisely describe, classify, and understand relationships among types of two- and three-dimensional objects using their defining properties.
Use visualization, spatial reasoning, and geometric modeling to solve problems.
Use geometric models to represent and explain numerical and algebraic relationships.
Measurement (NCTM)
Apply appropriate techniques, tools, and formulas to determine measurements.
Select and apply techniques and tools to accurately find length, area, volume, and angle measures to appropriate levels of precision.
Develop strategies to determine the surface area and volume of selected prisms, pyramids, and cylinders.