Irrational Numbers
An irrational number is a number that cannot be expressed as a fraction of two integers and its decimal representation goes on forever without repeating. In other words, it cannot be written as a simple fraction.
Characteristics of Irrational Numbers
- Cannot be expressed as a simple fraction
- Have non-repeating, non-terminating decimal representations
- Examples include: √2, π (pi), and e (Euler's number)
Representations of Irrational Numbers
Irrational numbers can be represented in different forms, such as:
Examples of Irrational Numbers
Some common examples of irrational numbers are:
- √2 ≈ 1.41421356...
- π (pi) ≈ 3.14159265...
- e (Euler's number) ≈ 2.71828183...
Study Tips for Understanding Irrational Numbers
To better understand irrational numbers, consider the following study tips:
- Practice estimating the values of irrational numbers using their decimal approximations.
- Explore the concept of square roots and their connection to irrational numbers.
- Use visual aids, such as number lines and geometric representations, to illustrate irrational numbers.
- Compare and contrast irrational numbers with rational numbers to understand their differences.
◂Math Worksheets and Study Guides Fourth Grade. Perimeter
Study Guide Perimeter
Perimeter  Activity Lesson
Activity Lesson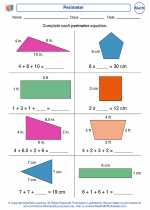 Perimeter
Perimeter  Activity Lesson
Activity Lesson Polygon Perimeter
Polygon Perimeter  Activity Lesson
Activity Lesson Amazing Areas
Amazing Areas  Worksheet/Answer key
Worksheet/Answer key Perimeter
Perimeter  Worksheet/Answer key
Worksheet/Answer key Perimeter
Perimeter  Worksheet/Answer key
Worksheet/Answer key Perimeter
Perimeter  Worksheet/Answer key
Worksheet/Answer key Dot to Dot
Dot to Dot  Worksheet/Answer key
Worksheet/Answer key Triangle Inequality Theorem
Triangle Inequality Theorem  Worksheet/Answer key
Worksheet/Answer key Park Perimeter
Park Perimeter  Worksheet/Answer key
Worksheet/Answer key Polygon Perimeters
Polygon Perimeters  Vocabulary/Answer key
Vocabulary/Answer key Perimeter
Perimeter 

 Activity Lesson
Activity Lesson
 Activity Lesson
Activity Lesson
 Activity Lesson
Activity Lesson
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Worksheet/Answer key
Worksheet/Answer key
 Vocabulary/Answer key
Vocabulary/Answer key

The resources above cover the following skills:
Geometry (NCTM)
Analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships.
Identify, compare, and analyze attributes of two- and three-dimensional shapes and develop vocabulary to describe the attributes.
Use visualization, spatial reasoning, and geometric modeling to solve problems.
Use geometric models to solve problems in other areas of mathematics, such as number and measurement.